null - 程序员宅基地

如何理解最小二乘法？-程序员宅基地

最小平方法是十九世纪统计学的主题曲。从许多方面来看, 它之于统计学就相当于十八世纪的微积分之于数学。
----乔治·斯蒂格勒的《The History of Statistics》

1 日用而不知

来看一个生活中的例子。比如说，有五把尺子：

用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

$\begin{array}{c|c} \qquad\qquad&\qquad长度\qquad\\\hline \color{red}红& 10.2 \\\hline \color{blue}蓝& 10.3 \\\hline \color{orange}橙&9.8\\\hline \color{Goldenrod}黄&9.9\\\hline \color{green}绿&9.8\\\end{array}$

之所以出现不同的值可能因为：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$

日常中就是这么使用的。可是作为很事'er的数学爱好者，自然要想下：

这样做有道理吗？
用调和平均数行不行？
用中位数行不行？
用几何平均数行不行？

2 最小二乘法

换一种思路来思考刚才的问题。

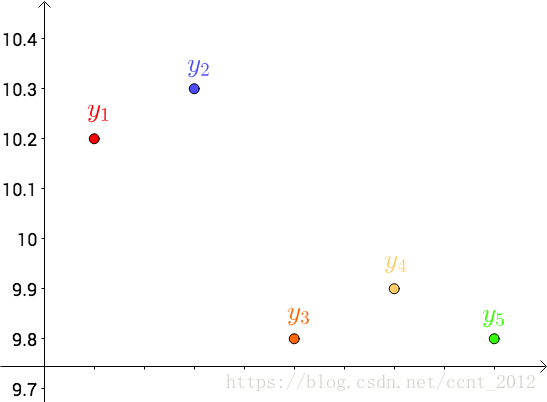
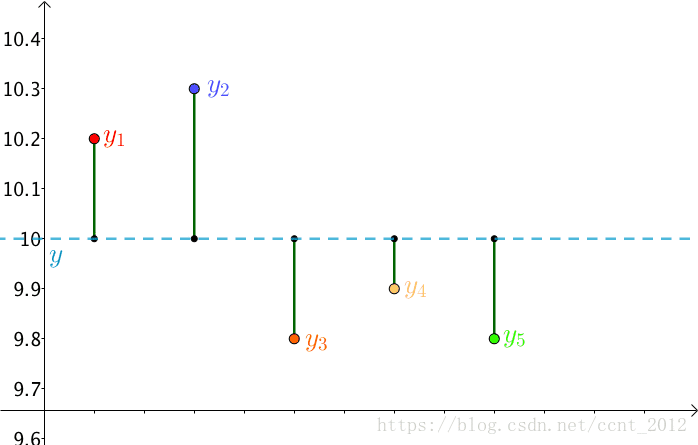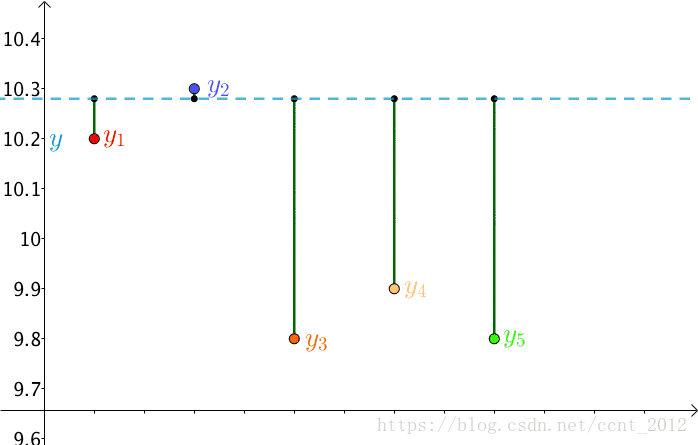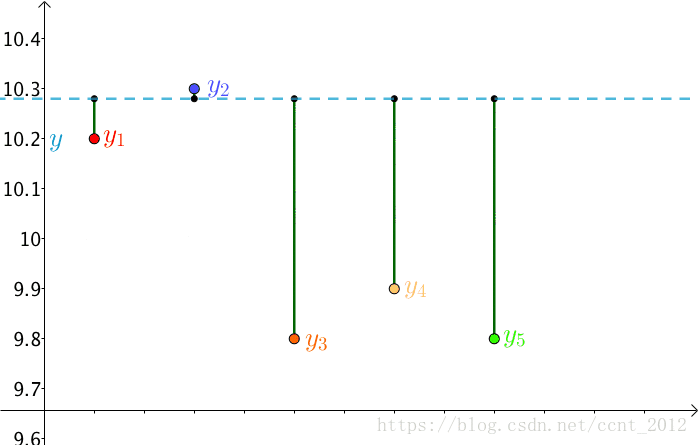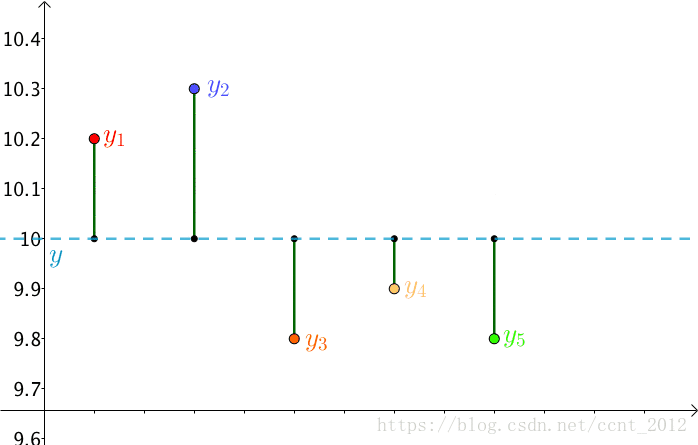
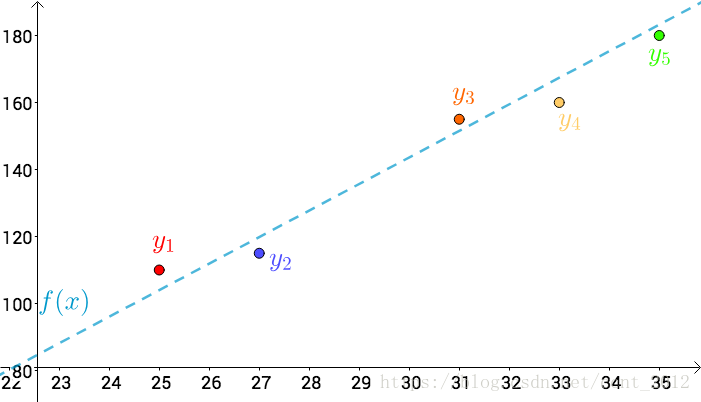
首先，把测试得到的值画在笛卡尔坐标系中，分别记作 $y_i$ ：

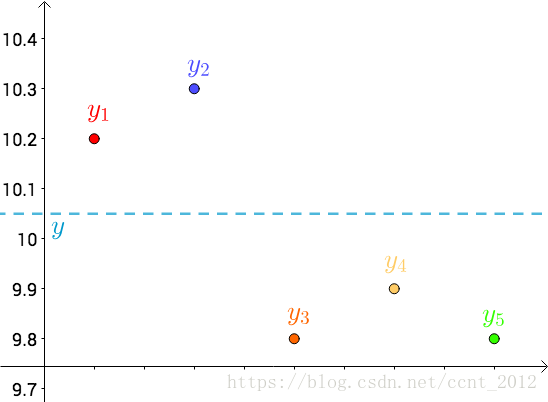
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$ ：

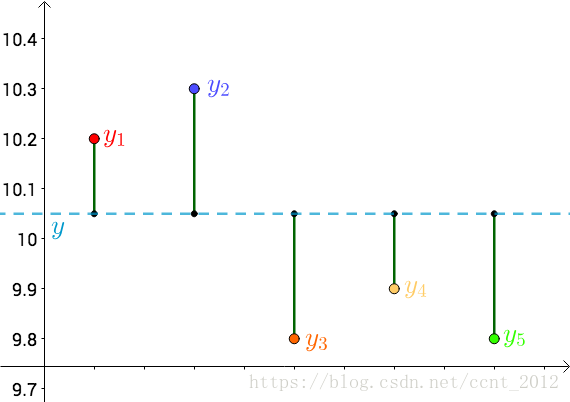
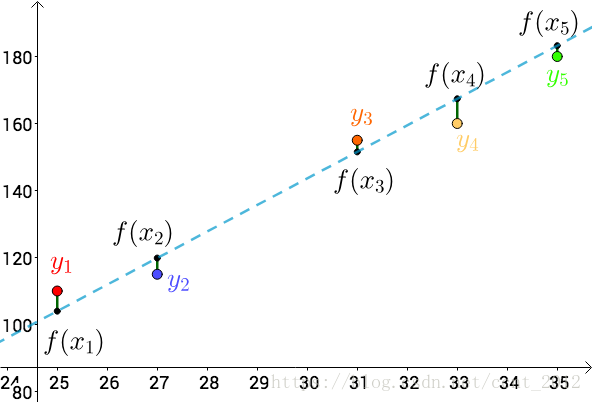
每个点都向 $y$ 做垂线，垂线的长度就是 $|y-y_i|$ ，也可以理解为测量值和真实值之间的误差：

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$|y-y_i|\to (y-y_i)^2$

总的误差的平方就是：

$\epsilon=\sum (y-y_i)^2$

因为 $y$ 是猜测的，所以可以不断变换：

自然，总的误差 $\epsilon$ 也是在不断变化的。

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$ 就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动（关于这点可以看下“如何理解无偏估计？”）。

这就是最小二乘法，即：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

这个猜想也蛮符合直觉的，来算一下。

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$\begin{aligned} \frac{d}{dy}\epsilon &=\frac{d}{dy}\sum (y-y_i)^2=2\sum (y-y_i)\\ \quad\\ &=2((y-y_1)+(y-y_2)+(y-y_3)+(y-y_4)+(y-y_5))=0 \quad\\\end{aligned}$

进而：

$5y=y_1+y_2+y_3+y_4+y_5\implies y=\frac{y_1+y_2+y_3+y_4+y_5}{5}$

正好是算术平均数。

原来算术平均数可以让误差最小啊，这下看来选用它显得讲道理了。

以下这种方法：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

3 推广

算术平均数只是最小二乘法的特例，适用范围比较狭窄。而最小二乘法用途就广泛。

比如温度与冰淇淋的销量：

$\begin{array}{c|c} \qquad\qquad&\qquad销量\qquad\\\hline \color{red}{25^\circ}& 110 \\\hline \color{blue}{27^\circ}& 115 \\\hline \color{orange}{31^\circ}&155\\\hline \color{Goldenrod}{33^\circ}&160\\\hline \color{green}{35^\circ}&180\\\end{array}$

看上去像是某种线性关系：

可以假设这种线性关系为：

$f(x)=ax+b$

通过最小二乘法的思想：

上图的 $i,x,y$ 分别为：

$\begin{array}{c|c|c} \qquad i\qquad&\qquad x\qquad&\qquad y\qquad\\\hline 1&25& 110 \\\hline 2&27& 115 \\\hline 3&31&155\\\hline 4&33&160\\\hline 5&35&180\\\end{array}$

总误差的平方为：

$\epsilon=\sum (f(x_i)-y_i)^2=\sum (ax_i+b-y_i)^2$

不同的 $a,b$ 会导致不同的 $\epsilon$ ，根据多元微积分的知识，当：

$\begin{cases} \frac{\partial}{\partial a}\epsilon=2\sum (ax_i+b-y_i)x_i=0\\ \quad\\ \frac{\partial}{\partial b}\epsilon=2\sum (ax_i+b-y_i)=0\end{cases}$

这个时候 $\epsilon$ 取最小值。

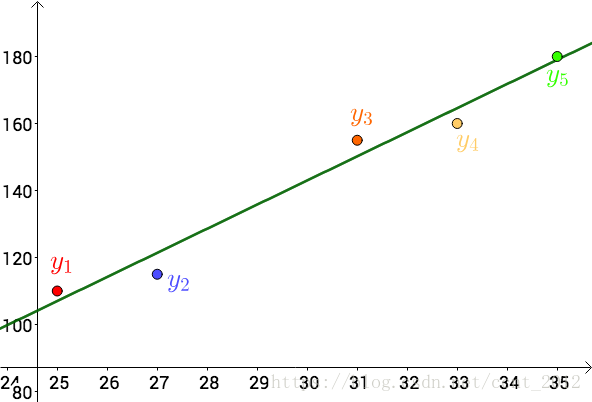
对于 $a,b$ 而言，上述方程组为线性方程组，用之前的数据解出来：

$\begin{cases} a\approx 7.2\\ \quad\\ b\approx -73\end{cases}$

也就是这根直线：

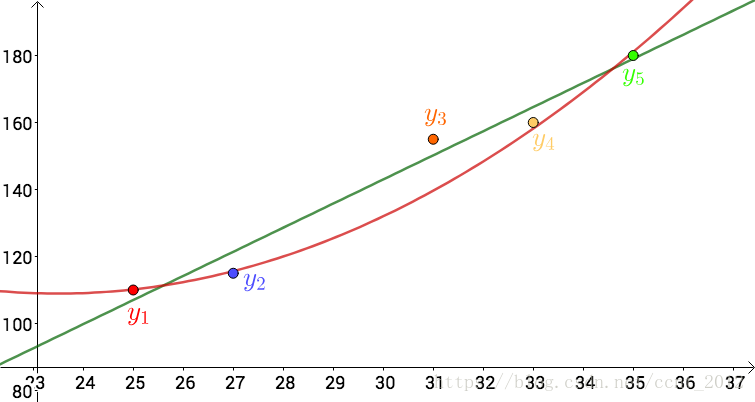
其实，还可以假设：

$f(x)=ax^2+bx+c$

在这个假设下，可以根据最小二乘法，算出 $a,b,c$ ，得到下面这根红色的二次曲线：

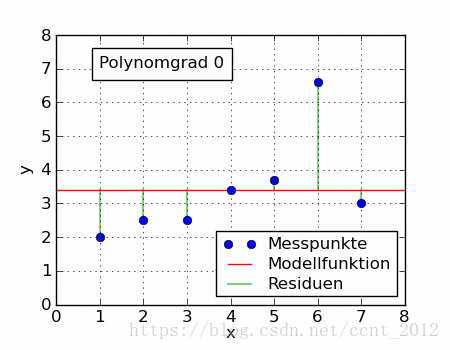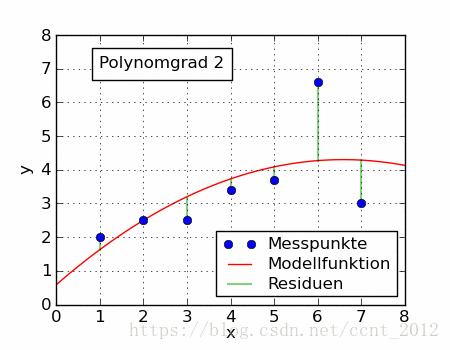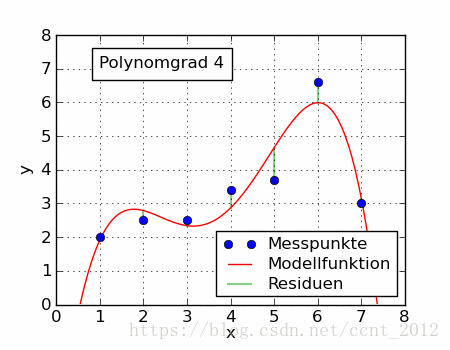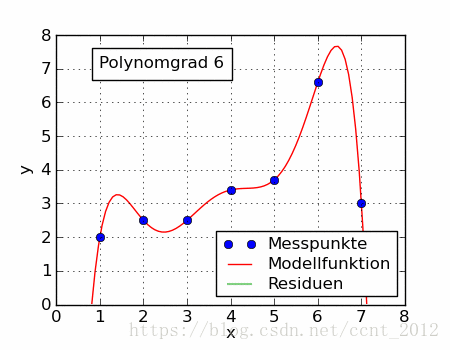
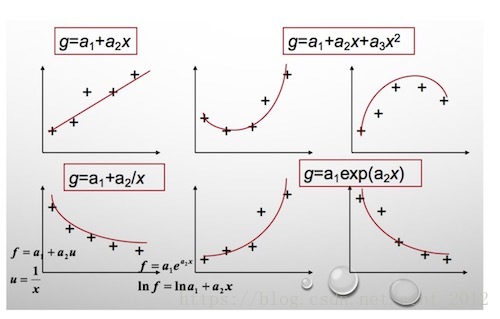
同一组数据，选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线（出处）：

不同的数据，更可以选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线：

$f(x)$ 也不能选择任意的函数，还是有一些讲究的，这里就不介绍了。

4 最小二乘法与正态分布

我们对勒让德的猜测，即最小二乘法，仍然抱有怀疑，万一这个猜测是错误的怎么办？

数学王子高斯（1777－1855）也像我们一样心存怀疑。

高斯换了一个思考框架，通过概率统计那一套来思考。

让我们回到最初测量线段长度的问题。高斯想，通过测量得到了这些值：

每次的测量值 $x_i$ 都和线段长度的真值 $x$ 之间存在一个误差：

$\epsilon_i=x-x_i$

这些误差最终会形成一个概率分布，只是现在不知道误差的概率分布是什么。假设概率密度函数为：

$p(\epsilon)$

再假设一个联合概率密度函数，这样方便把所有的测量数据利用起来：

$\begin{aligned} L(x) &=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\ \quad\\ &=p(x-x_i)p(x-x_2)\cdots p(x-x_5)\end{aligned}$

讲到这里，有些同学可能已经看出来了上面似然函数了（关于似然函数以及马上要讲到的极大似然估计，可以参考“如何理解极大似然估计法？”）。

因为 $L(x)$ 是关于 $x$ 的函数，并且也是一个概率密度函数（下面分布图形是随便画的）：

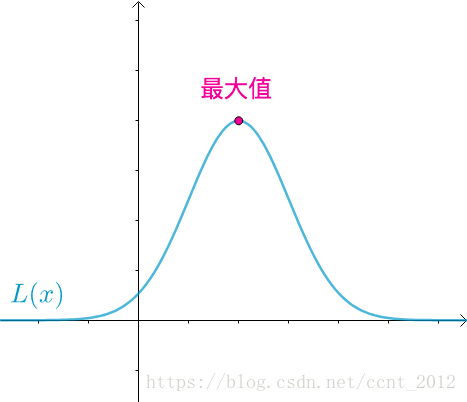
根据极大似然估计的思想，概率最大的最应该出现（既然都出现了，而我又不是“天选之才”，那么自然不会是发生了小概率事件），也就是应该取到下面这点：

当下面这个式子成立时，取得最大值：

$\frac{d}{dx}L(x)=0$

然后高斯想，最小二乘法给出的答案是：

$x=\overline{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$

如果最小二乘法是对的，那么 $x=\overline{x}$ 时应该取得最大值，即：

$\frac{d}{dx}L(x)|_{x=\overline{x}}=0$

好，现在可以来解这个微分方程了。最终得到：

$p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

这是什么？这就是正态分布啊。

并且这还是一个充要条件：

$x=\overline{x}\iff p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

也就是说，如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。

那么误差的分布是正态分布吗？

我们相信，误差是由于随机的、无数的、独立的、多个因素造成的，比如之前提到的：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

那么根据中心极限定理（参考“为什么正态分布如此常见？”），误差的分布就应该是正态分布。

因为高斯的努力，才真正奠定了最小二乘法的重要地位。

文章最新版本在（有可能会有后续更新）：如何理解最小二乘法？

本文链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

ES6笔记--深度克隆（深拷贝和浅拷贝）_ed6深克隆-程序员宅基地

文章浏览阅读1.6k次。深度克隆（深拷贝和浅拷贝）拷贝数据：基本数据类型：拷贝后会生成一份新的数据，修改拷贝以后的数据不会影响原数据对象/数组拷贝后不会生成新的数据，而是拷贝引用，修改拷贝后的数据会影响原数据拷贝数据的方法：1.直接赋值给一个变量：浅拷贝修改拷贝以后的数据会影响原数据2.Object.assign():浅拷贝3.Array.prototype.concat():浅拷贝,可用于合并数组，如果传值。4.Array.prototype.slice(startindex,endindex)：浅拷贝5._ed6深克隆

C++ primer -IO库-fstream-程序员宅基地

文章浏览阅读277次，点赞7次，收藏8次。每次写操作前，均定位到文件末尾，不会截断文件，需要将内容添加到文件末尾时，应添加该模式，例：ofstrm.open("文件名", ofstream::app) 或 ofstrm.open("文件名", ofstream::out | ofstream::app)对于fstream和sstream，它们继承了iostream，因此接口支持iostream时，也支持使用fstream和sstream。以上是处理char字符的类型，对于宽字符类型，有wfstream/wifstream/wofstream。

机械优化设计进退法c语言程序,机械优化设计c语言程序讲解.doc-程序员宅基地

文章浏览阅读64次。计算 f(x1,x2)=x^2+x1^2-x0*x1-10*x0-4*x1+60#include "stdio.h"#include "stdlib.h"#include "math.h"double objf(double x[]){double ff;ff=x[0]*x[0]+x[1]*x[1]-x[0]*x[1]-10*x[0]-4*x[1]+60;return(ff);}void jtf(..._机械优化设计进退法c语言程序

Vue3打印插件Print.js的使用_vue3 print-js-程序员宅基地

文章浏览阅读1.8k次，点赞18次，收藏25次。如何认识和快速上手 `Print.js`，我们可以从官网的内容开始阅读，在官网中有很详细的介绍和使用例子，虽然是英文版的。`Print.js` 打印插件包括了 `PDF` 打印、`HTML` 打印、`JSON` 打印、图像打印等。本人每篇文章都是一字一句码出来，希望对大家有所帮助，多提提意见。_vue3 print-js

YOLOV8 C++ opecv_dnn模块部署_opencv4.7 cudnn yolov8-程序员宅基地

YOLOV8 C++ opecv_dnn模块部署。opencv编译需时间久，GPU版本可实时，有问题私信留言。

JS获得token_js获取token-程序员宅基地

文章浏览阅读2.3w次。使用struts有一个很奇怪的事情，就是你不知道在什么时候，就放进来一个bug，重复地提交，而且渗透到好几个方法，甚至整个action都会被污染。像打补丁似的，struts本身可以有一个可以用来防止重复提交的拦截器: 虽然这个token能够有效地防止重复提交，但是也能够让你原来的架构一团糟。可以拿一个亲身经历作为教材。在一个搭了frame的框架里，左边的frame_js获取token

随便推点

Xshell如何上传文件_如何使用xshell上传文件-程序员宅基地

文章浏览阅读153次。/ 上传文件，单机选中上传的文件。_如何使用xshell上传文件

xml报文转Java实体_xml字符串转换为实体对象-程序员宅基地

文章浏览阅读1.4k次。因为需要对接一些比较老的系统接口，他们的请求方式不是JSON数据结构，一般会采用xml数据结构来作为数据的入参和返参。因为我们的系统是通过JSON数据进行交互的突然接入xml数据结构的会比较的麻烦，麻烦的体现在xml数据结构比较复杂，同时如果采用字符串拼接的话会比较的难以维护。通过JAXBContext来将xml字符串转为Java实体或者把Java实体转为xml字符串_xml字符串转换为实体对象

关于形如--error LNK2005: xxx 已经在 msvcrtd.lib ( MSVCR90D.dll ) 中定义--的问题分析解决_error lnk2005: __lock 已经在 msvcrtd.lib(msvcr120d.dl-程序员宅基地

文章浏览阅读604次。http://www.cnblogs.com/qinfengxiaoyue/archive/2013/02/01/2889668.html--原文1.问题引出很久没有写程序设计入门知识的相关文章了，这篇文章要来谈谈程序库 (Library) 链接，以及关于 MSVC 与 CRT 之间的种种恩怨情仇。如果你使用的操作系统是 Linux、Mac 或其他非 Windo_error lnk2005: __lock 已经在 msvcrtd.lib(msvcr120d.dll) 中定义

org.springframework.beans.factory.BeanCreationException: Error creating bean...-程序员宅基地

文章浏览阅读527次。报错信息：org.springframework.beans.factory.BeanCreationException: Error creating bean with name 'initService' defined in file [E:\WebWork\SMS\WebRoot\WEB-INF\classes\applicationContext-service.xml]: I..._rg.springframework.beans.factory.beancreationexception: error creating bean

JavaScript版本一览_javascript的版本是写在拿的-程序员宅基地

文章浏览阅读1.5k次。JavaScript 1.0这是JavaScript的第一个发布版本，由Brendan Eich开发，并在1996年3月伴随Netscape公司的Navigator 2.0一起发布。JavaScript 1.1这个版本包含在1996年8月发布的Netscape Navigator 3.0中。ECMA-262第一版就是以这个版本为基础编写的。JavaScript 1.2Netscape Naviga_javascript的版本是写在拿的

oracle忘记密码_oracle密码忘记了-程序员宅基地

文章浏览阅读1.9k次。打开一个终端窗口（cmd），输入以下命令进入SQL*Plus。3、查看用户（知道要修改用户名的跳过）_oracle密码忘记了