欧拉法求解微分方程_欧拉法解微分方程-程序员宅基地
文章目录
欧拉法是一种求解微分方程的数值方法。微分方程的目标是求出方程的具体表达式,但数值方法则是根据方程求出其每一个点,而不是找出表达式,在工程上具有很大的实用性。
欧拉法求解微分方程组的原理
设有微分方程:
d x ( t ) d t = f ( x ) \frac{dx(t)}{dt} = f(x) dtdx(t)=f(x)
x ( t 0 ) = x 0 x(t_0)=x_0 x(t0)=x0已知。
我们对上述方程进行积分,积分区域为 [ t 0 , t 1 ] , Δ t = t 1 − t 0 [t_0,t_1],\Delta t = t_1-t_0 [t0,t1],Δt=t1−t0,可得:
x ( t 1 ) = x ( t 0 ) + ∫ t 0 t 1 f ( t ) d t x(t_1)=x(t_0)+\int_{t_0}^{t_1}f(t)dt x(t1)=x(t0)+∫t0t1f(t)dt
其中 x ( t 1 ) x(t_1) x(t1)就是我们要求解的东西了。于是,就差积分怎么解决了。
对于欧拉法来说,积分是靠梯形面积来近似,如下所示:
∫ t 0 t 1 f ( t ) d t = f ( x ( t 0 ) ) ( t 1 − t 0 ) = f ( x 0 ) Δ t \int_{t_0}^{t_1}f(t)dt = f(x(t_0))(t_1-t_0)=f(x_0)\Delta t ∫t0t1f(t)dt=f(x(t0))(t1−t0)=f(x0)Δt
带入上述方程即可得:
x ( t 1 ) = x ( t 0 ) + f ( x 0 ) Δ t x(t_1)=x(t_0)+f(x_0)\Delta t x(t1)=x(t0)+f(x0)Δt
按照上式进行递推,即可得:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
其中 x 0 x_0 x0 已知。问题就搞定了。
*欧拉法原理图解
因为
f ( x k ) = d x d t ∣ t = t k f(x_k) = \frac{dx}{dt}|_{t=t_k} f(xk)=dtdx∣t=tk
所以递推式可以写成:
x k + 1 = x k + d x d t ∣ t = t k Δ t x_{k+1} = x_{k} + \frac{dx}{dt}|_{t=t_k}\Delta t xk+1=xk+dtdx∣t=tkΔt
而 d x d t \frac{dx}{dt} dtdx是所求方程 x ( t ) x(t) x(t)的斜率,因此实际上是将下图的阴影部分的面积来替代积分表达式:

欧拉法数值稳定性讨论
方便讨论,我们取一种简单情况,设有微分方程:
d x ( t ) d t = a x \frac{dx(t)}{dt} = ax dtdx(t)=ax
什么是数值稳定性问题?
假设 k 步计算中, x k x_k xk与实际值存在误差 ρ k \rho_k ρk,则第 k+1 步计算中,误差是否会增大。若是,则不稳定啦。因为越往后计算,这个误差肯定是越爆炸的。
那么欧拉法数值稳定性如何呢?首先假设 x k x_k xk与实际值存在误差 ρ k \rho_k ρk,根据递推公式:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
设 f ( x k ) = a x k f(x_{k})=ax_{k} f(xk)=axk而:
x ^ k = x k + ρ k \hat{x}_k = x_k + \rho_{k} x^k=xk+ρk
故第 k+1 步时时:
x ^ k = ( 1 + a Δ t ) ( x k + ρ k ) = x k + 1 + ( 1 + a Δ t ) ρ k \hat{x}_k = (1+a\Delta t)(x_k+\rho_k)=x_{k+1}+(1+a\Delta t)\rho_k x^k=(1+aΔt)(xk+ρk)=xk+1+(1+aΔt)ρk
于是 k+1 步的误差为:
ρ k + 1 = ( 1 + a Δ t ) ρ k \rho_{k+1} = (1+a\Delta t)\rho_k ρk+1=(1+aΔt)ρk
若要求稳定,则必须有 ∣ 1 + a Δ t ∣ ≤ 1 |1+a\Delta t| \leq 1 ∣1+aΔt∣≤1
于是可得欧拉法的数值稳定区域如下:

欧拉法误差分析——局部截断误差
微分方程 d x d t = f ( x ) \frac{dx}{dt} = f(x) dtdx=f(x),用欧拉法时,我们的迭代方程是:
x k = x k − 1 + f ( x k − 1 ) Δ t = x k − 1 + d x d t ∣ t k − 1 Δ t x_{k} = x_{k-1} + f(x_{k-1})\Delta t =x_{k-1} + \frac{dx}{dt}|_{t_{k-1}}\Delta t xk=xk−1+f(xk−1)Δt=xk−1+dtdx∣tk−1Δt。
若对 x k x_{k} xk 进行泰勒展开,可得:
x ( t k ) = x ( t k − 1 + Δ t ) = x k − 1 + x ′ ( t k − 1 Δ t + x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x(t_{k}) = x(t_{k-1}+\Delta t) = x_{k-1} + x^{\prime}(t_{k-1} \Delta t + x^{\prime\prime}(t_{k-1}) \Delta t^2 + \cdots x(tk)=x(tk−1+Δt)=xk−1+x′(tk−1Δt+x′′(tk−1)Δt2+⋯
因此,欧拉法的截断误差为:
x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x^{\prime\prime}(t_{k-1}) \Delta t^2+ \cdots x′′(tk−1)Δt2+⋯
由于有 Δ t 2 \Delta t^2 Δt2,所以我称欧拉法的精度为 2-1 = 1 阶。
改进欧拉法原理
欧拉法是用梯形的面积来近似积分的,而且梯形的上底是用 KaTeX parse error: Expected 'EOF', got '}' at position 7: x_[i-1}̲时,曲线 x ( t ) x(t) x(t)的斜率来近似计算的,所以不太好,可以看到的是,欧拉法的精度只有一阶,其阶段误差与 Δ t 2 \Delta t^2 Δt2有关。这个误差之所以那么大,是因为我们在求积分(面积)的时候,用了以 x k − 1 x_{k-1} xk−1为上底的梯形去近似他。因此,我们需要对这个梯形的上底进行一定的修正。
首先,根据递推公式求出:
x k ( 0 ) = x k − 1 + f ( x k − 1 ) Δ t x_{k}^{(0)} = x_{k-1} + f(x_{k-1}) \Delta t xk(0)=xk−1+f(xk−1)Δt
之后再求出修正后的 x k x_{k} xk:
x k = x k − 1 + 1 2 ( f ( x k − 1 + x k ( 0 ) ) Δ t x_k = x_{k-1}+\frac{1}{2}(f(x_{k-1}+x_{k}^{(0)})\Delta t xk=xk−1+21(f(xk−1+xk(0))Δt
其原理图如下:
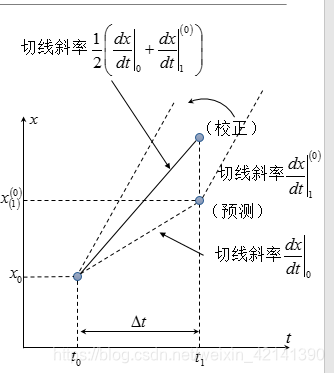
改进欧拉法的稳定性分析
设微分方程为 d x d t = λ x \frac{dx}{dt} = \lambda x dtdx=λx,于是KaTeX parse error: Undefined control sequence: \ambda at position 16: x_{k}^{(0)]=(1+\̲a̲m̲b̲d̲a̲\Delta t)x_{k-1…, f ( x k ( 0 ) = λ ( 1 + λ Δ t ) x k − 1 f(x_{k}^{(0)}=\lambda(1+\lambda\Delta t)x_{k-1} f(xk(0)=λ(1+λΔt)xk−1,于是 x k = ( 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ) x k − 1 x_{k} = (1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2)x_{k-1} xk=(1+λΔt+21(λΔt)2)xk−1
所以误差不增值的条件为: ∣ 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ∣ ≤ 1 |1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2|\leq1 ∣1+λΔt+21(λΔt)2∣≤1,表现在图上,即为:
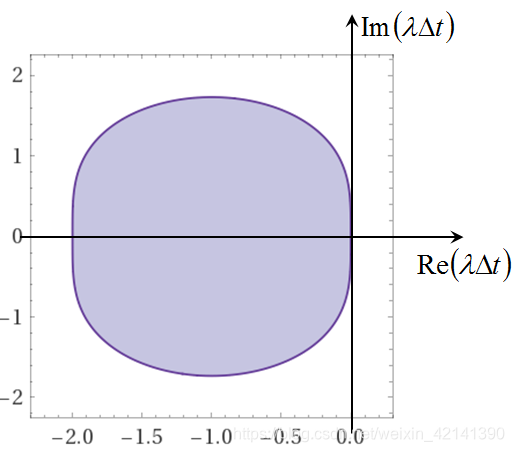
对比欧拉法,显然稳定区域大了一点。
改进欧拉法的误差分析
因为 f ( x k 0 ) = d x d t ∣ x k − 1 + d 2 x d t 2 ∣ x k − 1 Δ t 2 + O ( Δ t 2 ) f(x_{k}^{0}) = \frac{dx}{dt}|_{x_{k-1}}+\frac{d^{2}x}{dt^2}|_{x_{k-1}}\Delta t^2+O(\Delta t^2) f(xk0)=dtdx∣xk−1+dt2d2x∣xk−1Δt2+O(Δt2)
于是 x k = x k − 1 + d x d t ∣ x k − 1 Δ t + d 2 x d t 2 ∣ x k − 1 Δ t 2 x_{k} = x_{k-1}+\frac{dx}{dt}|_{x_{k-1}}\Delta t+\frac{d^2x}{dt^2}|_{x_{k-1}}\Delta t^2 xk=xk−1+dtdx∣xk−1Δt+dt2d2x∣xk−1Δt2
对比泰勒展开,可知其误差为 O ( Δ t 3 ) O(\Delta t^3) O(Δt3),因此精确度为 3-1 = 2阶!
隐式梯形法
隐式梯形法也是利用 x k x_k xk 来改善上底,只是其递推公式为:
x k = x k − 1 + Δ t 2 ( f ( x k − 1 ) + f ( x k ) ) x_{k} = x_{k-1} + \frac{\Delta t}{2}(f(x_{k-1})+f(x_{k})) xk=xk−1+2Δt(f(xk−1)+f(xk))
因此,上底的修正,包含在上述方程中。因此,不同于欧拉法,每一次迭代,隐式梯形法都要求解一次代数方程。
隐式梯形法的稳定性和误差
首先是稳定性,同样对于微分方程 d x d t = λ x \frac{dx}{dt}=\lambda x dtdx=λx,可得其误差的表达式为:
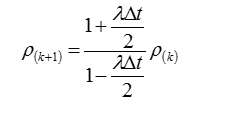
误差不增值条件: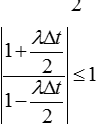
整理可得: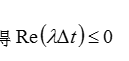
因此其稳定区域为:复平面的左半部分,可见比改进欧拉发、欧拉法要大得多!!
至于误差,同样可以证明的是隐式梯形法的精确度为2阶。
案例
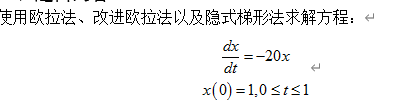
可见求解区域为 [0,1],我们设置求解的步数为 100,也即 Δ t = 0.01 s \Delta t = 0.01s Δt=0.01s,代码如下:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -20*x
def uler(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = x[i]+f(x[i])*dt
x.append(xk)
return x,t
def uler2(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xkk = x[i]+f(x[i])*dt
xk = x[i]+ 1/2*(f(x[i])+f(xkk))*dt
x.append(xk)
return x,t
import sympy
x = sympy.symbols('x')
def uler3(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = (x[i]+dt*f(x[i])/2)/(1+10*dt)
x.append(xk)
return x,t
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
font1 = {
'family' : 'SimHei',
'weight' : 'normal',
'size' : 15,
}
def myplot(n,x0,t0,tn,f):
x1,t = uler(n,x0,t0,tn,f)
x2,t = uler2(n,x0,t0,tn,f)
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.plot(t,x1,linewidth=3,color='r',label='欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
plt.subplot(1,3,2)
plt.plot(t,x2,linewidth=3,color='b',label='改进欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
x3,t = uler3(n,x0,t0,tn,f)
plt.subplot(1,3,3)
plt.plot(t,x3,linewidth=3,color='g',label='隐式梯形法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
if __name__ == '__main__':
myplot(100,1,0,1,f)
求解结果:
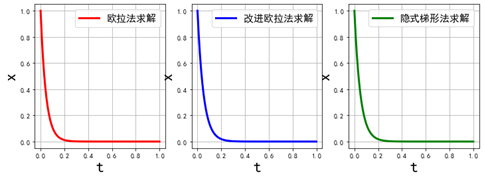
可以修改步长为 15,可得:
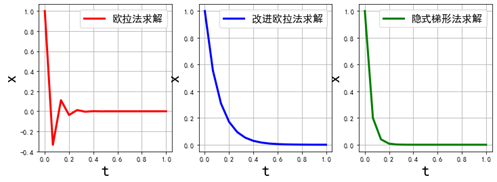
为什么步数为 15,结果就变形了呢?这是因为算法的稳定性、误差的原因,这里不再分析。
智能推荐
c# 调用c++ lib静态库_c#调用lib-程序员宅基地
文章浏览阅读2w次,点赞7次,收藏51次。四个步骤1.创建C++ Win32项目动态库dll 2.在Win32项目动态库中添加 外部依赖项 lib头文件和lib库3.导出C接口4.c#调用c++动态库开始你的表演...①创建一个空白的解决方案,在解决方案中添加 Visual C++ , Win32 项目空白解决方案的创建:添加Visual C++ , Win32 项目这......_c#调用lib
deepin/ubuntu安装苹方字体-程序员宅基地
文章浏览阅读4.6k次。苹方字体是苹果系统上的黑体,挺好看的。注重颜值的网站都会使用,例如知乎:font-family: -apple-system, BlinkMacSystemFont, Helvetica Neue, PingFang SC, Microsoft YaHei, Source Han Sans SC, Noto Sans CJK SC, W..._ubuntu pingfang
html表单常见操作汇总_html表单的处理程序有那些-程序员宅基地
文章浏览阅读159次。表单表单概述表单标签表单域按钮控件demo表单标签表单标签基本语法结构<form action="处理数据程序的url地址“ method=”get|post“ name="表单名称”></form><!--action,当提交表单时,向何处发送表单中的数据,地址可以是相对地址也可以是绝对地址--><!--method将表单中的数据传送给服务器处理,get方式直接显示在url地址中,数据可以被缓存,且长度有限制;而post方式数据隐藏传输,_html表单的处理程序有那些
PHP设置谷歌验证器(Google Authenticator)实现操作二步验证_php otp 验证器-程序员宅基地
文章浏览阅读1.2k次。使用说明:开启Google的登陆二步验证(即Google Authenticator服务)后用户登陆时需要输入额外由手机客户端生成的一次性密码。实现Google Authenticator功能需要服务器端和客户端的支持。服务器端负责密钥的生成、验证一次性密码是否正确。客户端记录密钥后生成一次性密码。下载谷歌验证类库文件放到项目合适位置(我这边放在项目Vender下面)https://github.com/PHPGangsta/GoogleAuthenticatorPHP代码示例://引入谷_php otp 验证器
【Python】matplotlib.plot画图横坐标混乱及间隔处理_matplotlib更改横轴间距-程序员宅基地
文章浏览阅读4.3k次,点赞5次,收藏11次。matplotlib.plot画图横坐标混乱及间隔处理_matplotlib更改横轴间距
docker — 容器存储_docker 保存容器-程序员宅基地
文章浏览阅读2.2k次。①Storage driver 处理各镜像层及容器层的处理细节,实现了多层数据的堆叠,为用户 提供了多层数据合并后的统一视图②所有 Storage driver 都使用可堆叠图像层和写时复制(CoW)策略③docker info 命令可查看当系统上的 storage driver主要用于测试目的,不建议用于生成环境。_docker 保存容器
随便推点
网络拓扑结构_网络拓扑csdn-程序员宅基地
文章浏览阅读834次,点赞27次,收藏13次。网络拓扑结构是指计算机网络中各组件(如计算机、服务器、打印机、路由器、交换机等设备)及其连接线路在物理布局或逻辑构型上的排列形式。这种布局不仅描述了设备间的实际物理连接方式,也决定了数据在网络中流动的路径和方式。不同的网络拓扑结构影响着网络的性能、可靠性、可扩展性及管理维护的难易程度。_网络拓扑csdn
JS重写Date函数,兼容IOS系统_date.prototype 将所有 ios-程序员宅基地
文章浏览阅读1.8k次,点赞5次,收藏8次。IOS系统Date的坑要创建一个指定时间的new Date对象时,通常的做法是:new Date("2020-09-21 11:11:00")这行代码在 PC 端和安卓端都是正常的,而在 iOS 端则会提示 Invalid Date 无效日期。在IOS年月日中间的横岗许换成斜杠,也就是new Date("2020/09/21 11:11:00")通常为了兼容IOS的这个坑,需要做一些额外的特殊处理,笔者在开发的时候经常会忘了兼容IOS系统。所以就想试着重写Date函数,一劳永逸,避免每次ne_date.prototype 将所有 ios
如何将EXCEL表导入plsql数据库中-程序员宅基地
文章浏览阅读5.3k次。方法一:用PLSQL Developer工具。 1 在PLSQL Developer的sql window里输入select * from test for update; 2 按F8执行 3 打开锁, 再按一下加号. 鼠标点到第一列的列头,使全列成选中状态,然后粘贴,最后commit提交即可。(前提..._excel导入pl/sql
Git常用命令速查手册-程序员宅基地
文章浏览阅读83次。Git常用命令速查手册1、初始化仓库git init2、将文件添加到仓库git add 文件名 # 将工作区的某个文件添加到暂存区 git add -u # 添加所有被tracked文件中被修改或删除的文件信息到暂存区,不处理untracked的文件git add -A # 添加所有被tracked文件中被修改或删除的文件信息到暂存区,包括untracked的文件...
分享119个ASP.NET源码总有一个是你想要的_千博二手车源码v2023 build 1120-程序员宅基地
文章浏览阅读202次。分享119个ASP.NET源码总有一个是你想要的_千博二手车源码v2023 build 1120
【C++缺省函数】 空类默认产生的6个类成员函数_空类默认产生哪些类成员函数-程序员宅基地
文章浏览阅读1.8k次。版权声明:转载请注明出处 http://blog.csdn.net/irean_lau。目录(?)[+]1、缺省构造函数。2、缺省拷贝构造函数。3、 缺省析构函数。4、缺省赋值运算符。5、缺省取址运算符。6、 缺省取址运算符 const。[cpp] view plain copy_空类默认产生哪些类成员函数