1.FFT介绍

\qquad 离散傅里叶变换（DFT）和卷积是信号处理中两个最基本也是最常用的运算，对于N点序列$x(n)$,其DFT变换对定义为：

$$\begin{gathered} X(k)=\sum _{n=0}^{N-1}x(n)W_N^{nk}k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi }{N}} \\ x(n)=\frac{1}{N}\sum _{k=0}^{N-1}X(k)W_N^{-nk}n=0,1,...,N-1 \end{gathered}$$
首先解释一下，这里的$W_N=e^{-j\frac{2\pi }{N}}$是一个复数运算，其取得过程如下所示：

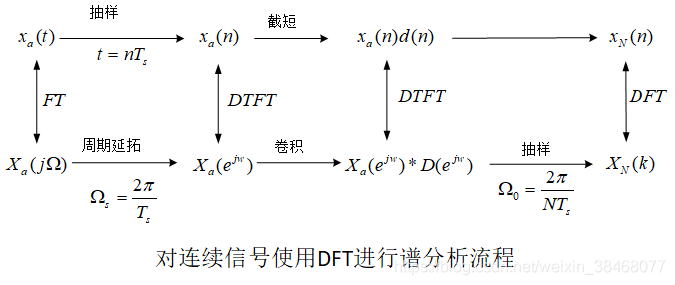
在上图中我们可以知道，这里的$W_N$是经过截短了的。
\qquad 另外在上边的公式中，我们可以看出，由于$W_N$是个复数，又因为k的取值范围在0到N-1，共有N个不同的选择，而对于每一个选定$k$值的式子，其$n$的取值范围又从0到N-1，由此可以算出，这$N$个点$X(k)$需要$N^2$次复数运算和$N(N-1)$次复数加法。再由欧拉公式：
$$\begin{gathered} e^{jw}=cosw+jsinw \\ {e}^{-jw}=cosw-jsinw \end{gathered}$$
将欧拉公式带入$W_N$则有：
$$W_N=e^{-j\frac{\pi }{2}}=cos(\frac{\pi }{2})-jsin(\frac{\pi }{2})=-j$$
由以上公式则也可以分别求得$W_N^{nk}$,当N等于4时，其表格如下所示：

$W_N^{nk}$ 取N=4	Value
$W_N^0$	$1$
$W_N^1$	$-j$
$W_N^2$	$-1$
$W_N^3$	$j$
$W_N^4$	$1$
$W_N^6$	$-1$
$W_N^9$	$-j$

在上边的运算中我们可以看到，虽然要运行的运算次数有很多，但是结果却是有一定规律的：
$$\begin{gathered} W_N^0=W_N^4=1 \\ {W}_N^1=W_N^9=-j \\ {W}_N^2=W_N^6=-1 \\ {W}_N^3=j \end{gathered}$$
\qquad 到了这里，我们或许就看出来了一些规律，此处我们取的N=4,我们发现其结果也是以4为周期的。那么我们现在给出其一般性规律，也就是我们后边的进行快速FFT的基础。
$$\begin{gathered} W_N^0=1 \\ {W}_N^{N/2}=-1 \\ {W}_N^{N+r}=W_N^r \\ {W}_N^{(N/2)+r}=-W_N^r \end{gathered}$$
\qquad 有了上边的规律，我们接下来就以4点DFT来测试一下，根据$X(k)$的计算公式直接计算的话，我们则需要进行$4^2=16$次的复数运算，所以我们根据以上得到的规律写成以下矩阵形式：
$$\left[\begin{array}{c}X(0)\\ X(1)\\ X(2)\\ X(3)\end{array}\right]=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& -j& -1& j\\ 1& -1& 1& -1\\ 1& j& -1& -j\end{array}\right]\left[\begin{array}{c}x(0)\\ x(1)\\ x(2)\\ x(3)\end{array}\right]$$
\qquad 接下来我们就要对上边的矩阵进行一下初等变换，使得其结果仍然等于等式左侧（这里的对右边两个矩阵进行初等变换的目的是为了更加直观的显示出蝶形运算）。
为方便表示，我接下来分别将等式右边的矩阵定义为矩阵A和矩阵B,其形式如下：
$$A=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& -j& -1& j\\ 1& -1& 1& -1\\ 1& j& -1& -j\end{array}\right]B=\left[\begin{array}{c}x(0)\\ x(1)\\ x(2)\\ x(3)\end{array}\right]$$
因为矩阵$AB=AEB$,则上边的$X(k)$的矩阵即可表示成：
$$\begin{gathered} \left[\begin{array}{c}X(0)\\ X(1)\\ X(2)\\ X(3)\end{array}\right]=A\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]B \\ =A\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]B \\ =\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& -1& -j& j\\ 1& 1& -1& -1\\ 1& -1& j& -j\end{array}\right]\left[\begin{array}{c}x(0)\\ x(2)\\ x(1)\\ x(3)\end{array}\right] \end{gathered}$$
\qquad 在上式中，我们对于矩阵A的第二列和第三列互换，将矩阵B的第二行和第三行互换，其结果不变。根据此结果，我们就可以的得出，如下等式：
$$\begin{gathered} X(0)=[x(0)+x(2)]+[x(1)+x(3)] \\ X(1)=[x(0)-x(2)]-[x(1)-x(3)]j \\ X(2)=[x(0)+x(2)]-[x(1)+x(3)] \\ X(3)=[x(0)-x(2)]+[x(1)-x(3)]j \end{gathered}$$
\qquad 这样，四点DFT实际上只需要进行一次复数乘法，也就是只需要进行计算$[x(1)-x(3)]j$即可，其实该问题的关键就是如何巧妙的利用W因子的周期性以及对称性，导出一个高效的快速算法。
\qquad 在上边的推导中，我们也可以看到在应用了快速傅里叶变换算法（FFT）后，使得N点的DFT算法的乘法计算量由$N^2$次运算降为$\frac{N}{2}lo{g}_{2}N$次，大大加快了计算速度。

2.时间抽取（DIT）基2 FFT算法

在介绍这个之前，我先介绍一下FFT的核心思想：

对于N点的DFT算法，我们习惯上使用$N=2^M$来进行计算，根据DFT正变换的公式:

$$X(k)=\sum _{n=0}^{N-1}x(n)W_N^{nk}k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi }{N}}$$
中我们将$x(n)$分为奇、偶两部分，也就是令$n=2r、n=2r+1r=0.1,...,\frac{N}{2}-1$于是上式也就可以改写为：
$$\begin{gathered} X(k)=\sum _{r=0}^{N/2-1}x(2r)W_N^{2rk}+\sum _{r=0}^{N/2-1}x(2r+1)W_N^{(2r+1)k} \\ =\sum _{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk}+\sum _{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k} \end{gathered}$$
式中$W_{N/2}=e^{-j\frac{2\pi }{N/2}}=e^{-j\pi }$
现在令$A(k)、B(k)$：分别代表$X(k)$的偶数项和奇数项：
$$\begin{gathered} A(k)=\sum _{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk}k=0,1,...,\frac{N}{2}-1 \\ B(k)=\sum _{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k}k=0,1,...,\frac{N}{2}-1 \end{gathered}$$
那么，$X(k)$则可以表示为：
$$X(k)=A(k)+W_N^{k}B(k),k=0,1,...,\frac{N}{2}-1$$
\qquad 但是此时我们仅可以根据该式子，算出来一半的$X(k)$,也就是$X(0)、X(1)$,而其余两项该式是无法求出的。具体的想要求出其余两项则需要公式：
$$\begin{gathered} X(k+\frac{N}{2})=A(k+\frac{N}{2})+W_N^{k+\frac{N}{2}}B(k+\frac{N}{2}) \\ =A(k+\frac{N}{2})-W_N^{k}B(k+\frac{N}{2}) \\ =A(k)-W_N^{k}B(k),k=0,1,...,\frac{N}{2}-1 \end{gathered}$$
\qquad 此处的$A(k+\frac{N}{2})$可以理解为偶数项的下一个周期，所以此处可以直接看为$A(k)$。
所以用$A(k)、B(k)$可以完整的表示$X(k)$,当N=4时，$A(k)、B(k)$以及$X(k)$的关系如下所示：

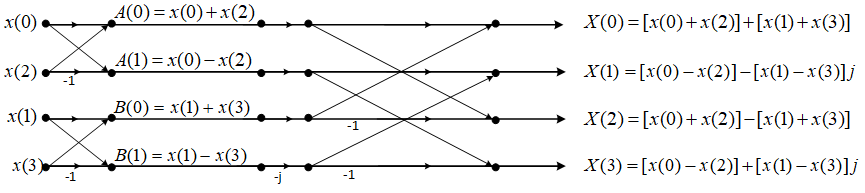
\qquad 这里我只展示了当N=4的时候，当N=8的时候，则我们需要继续将$A(k)$分为偶数项$C(k)$与奇数项$D(k)$之和，将$B(k)$分为偶数项$E(k)$与奇数项$F(k)$之和,其$k$值取值范围为$k=0,1,...,\frac{N}{4}-1$。
\qquad 若N=16，或者更高的幂，可以按照这样的方法继续分下去，直到分到两点的DFT为止。
介绍到这里，相信大家都已经很明白了，该算法是将时间$n$按照奇、偶分开，所以被称为时间抽取算法。

3.FFT算法的一般规律

\qquad 我们知道，对于进行FFT快速傅里叶变换，找到W因子的周期性以及对称性是非常关键的。比如当N=4的时候，$x(0)、x(1)、x(2)、x(3)$的排列顺序为$x(0)、x(2)、x(1)、x(3)$。如果这个顺序让我们自己取记忆的话，如果当N值小的时候或许还可以记住，但是如果当N大的时候，这样单纯记忆就显得不切实际。为此，我们能否找到它的排列规律显得尤为重要，以下我将分别以N=4和N=8来介绍这一方法：
当N=4时其表格如下：

$n$	$x(n)$	$X(k)$	$k$
0	00	000	0
2	10	001	1
1	01	010	2
3	11	011	3

当N=8时其表格如下：

$n$	$x(n)$	$X(k)$	$k$
0	000	000	0
4	100	001	1
2	010	010	2
6	110	011	3
1	001	100	4
5	101	101	5
3	011	110	6
7	111	111	7

仔细观看的话，我们或许会发现$x(n)$的取值顺序也是按照二进制加法，但是这个加法是在左侧加,而$X(k)$则是在右侧加。也就是说是$X(k)$的对称。有了这个规律，那么不管$N=2^M$的值取多大，我们都可以快速的排列出其顺序，这对于加快运算速度是有很大帮助的。

因为$M=lo{g}_{2}N$所以将N点DFT可以分成M级，当N等于8时，M=3,从左到右可以分为$m=0,m=1,m=2$三级。接下来我将展示8点DFT时间抽取算法的信号流图：

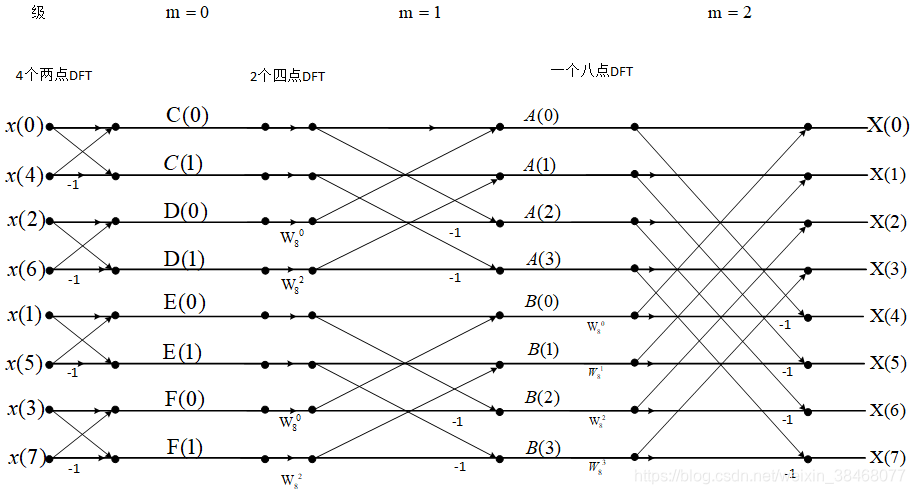
这里我们或许就会看到如下现象：

在每一个向上连接的线的下边都要乘一个$W^r$因子，
每一个向下连接的线的搭档都需要乘-1。

下面我将会来介绍一下$W^r$因子的分布情况:

$m$ 值（第几级）	对应的$W^r$因子分布
$m=0$ 级	$W_2^r,r=0$
$m=1$ 级	$W_4^r,r=0,1$
$m=2$ 级	$W_8^r,r=0,1,2,3$
…	…
$m=M-1$ 级	$W_N^r,r=0,1,...,\frac{N}{2}-1$

如果你仔细看我的流图的话或许会发现，我在m=1的时候，使用了因子$W_8^0，W_8^2$,在这里我使用这个因子只是为了方便和后边的比较，其实这个还是有一个代换公式的：
$$W_8^0=W_4^0，W_8^2=W_4^1$$

4.后续

该部分留作后边对于FFT的更加深入的理解。