---

三分用以解决单峰函数求峰值问题。

---

实数三分

实数三分模板：

double l = L, r = R;
while(r - l > 1e-7)
{
    
	double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
	if(check(lmid) < check(rmid)) l = lmid; //如果是中间凸的单峰函数是<号，中间凹是>号。
	else r = rmid;
}
printf("%.10f", l); //l为最佳位置，check(l)为峰值。

---

例1，模板题

Link
给出一个 $N$ 次函数，保证在范围 $[l,r]$ 内存在一点 $x$，使得 $[l,x]$ 上单调增，$[x,r]$ 上单调减。试求出 $x$ 的值。

思路
实数三分的模板题，每次将当前区间分成三段 [l, l+(r-l)/3], [l+(r-l)/3, r-(r-l)/3], [r-(r-l)/3, r]，根据分界点 l+(r-l)/3 和 r-(r-l)/3 时结果的大小，舍弃掉答案不在的那段，剩余两段。
所以三分到答案最近的整数的复杂度为 $O(2lo{g}_{3}n)$，近似于 $O(2logn)$。如果再精确范围到几位小数的话，复杂度相应增大。

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)

const int N = 200010, mod = 1e9+7;
int T, n, m;
double a[N];
double L, R;

double check(double x){
    
	double sum = 0;
	for(int i=0;i<=n;i++)
	{
    
		double t = 1;
		for(int j=1;j<=i;j++) t *= x;
		sum += a[i] * t;
	}
	return sum;
}

signed main(){
    
	Ios;
	cin >> n;
	cin >> L >> R;
	
	for(int i=n;i>=0;i--) cin >> a[i];
	
	double l = L, r = R;
	while(r - l > 1e-7)
	{
    
		double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) < check(rmid)) l = lmid;
		else r = rmid;
	}
	printf("%.10f", l);
	
	return 0;
}

例2，Party All the Time

Link
给定一维坐标系中的 n 个人，每人有位置 $x_i$ 和 重量 $w_i$。
如果所在位置为 $x_i$ 的人走到位置 $P$ 的话，花费为 $|P-x_i{|}^3\ast w_i$。
选定一个位置，使得所有人到这个位置的花费之和最小，输出最小和。

$1<=N<=5\ast 10^4,|x_i|<=10^6,0<w_i<15$

思路
直观上感觉，如果P位置太靠左的话，右边的点过来就要耗费更多花费，如果太靠右的话，左边的点过来就要耗费更多花费。最佳方案就是把 P 放到中间。
也就是说，总花费是一个中间凹的单峰函数。
所以可以三分位置，找到最佳位置。

Code

//http://acm.hdu.edu.cn/showproblem.php?pid=4355
#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)

const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
    
	double pos, w;
}a[N];

double check(double x)
{
    
	double sum = 0;
	for(int i=1;i<=n;i++)
	{
    
		double s = fabs(a[i].pos - x);
		sum += s * s * s * a[i].w;
	}
	return sum;
}

signed main(){
    
	scanf("%lld", &T);
	for(int cs = 1; cs <= T; cs ++)
	{
    
		scanf("%lld", &n);
		for(int i=1;i<=n;i++)
		{
    
			double x, w; scanf("%lf%lf", &x, &w);
			a[i] = {
    x, w};
		}
		
		double l = -1e6, r = 1e6;
		for(int i=1;i<=100;i++)
		{
    
			double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
			if(check(lmid) > check(rmid)) l = lmid;
			else r = rmid;
		}
		printf("Case #%lld: %.0f\n", cs, check(l));
	}
	
	return 0;
}

变式：P1883 函数

---

整数三分

就只需要将答案三分到最接近峰值的整数即可，但模板有些不同。

int l = 0, r = 1e9;
while(l < r)
{
    
	int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
	if(check(lmid) < check(rmid)) l = lmid + 1; 如果是中间凸的单峰函数是<号，中间凹是>号。
	else r = rmid - 1;
}
cout << check(l) << endl; //l为最佳位置，check(l)为峰值。

例1，E. Restorer Distance (+贪心)

Link
给定长度为 n 的整数数列，可以进行若干次下面操作：

• 将某个位置上的值 + 1，花费为 $A$；
• 将某个位置上的值 - 1，花费为 $R$；
• 选择两个位置 $i,j$，将 $a[i]-1,a[j]+1$，花费为 $M$。

问，使得所有数相同的最小花费为多少？

思路
如果将所有数都变得很小的话，那么原来很大的值要花费很多才能变过来；如果将所有数都变得很大的话，原来很小的值也要花费很多才能变过来。所以最佳方案就是把所有数变到中间的一个值。

花费之和 对于 最后变成的值 形成了一个中间凹的单峰函数。
三分最后变成的值，得到最小花费。

因为原来是整数，每次变化都使其+1或-1，所以最终变成的值也是整数，三分只考虑整数。

check 的时候贪心考虑，如果 M > A+R 的话就先用操作三，否则就只用操作一和二。

Code

//https://codeforces.com/problemset/problem/1355/E
#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
int cost1, cost2, cost3;

int check(int mid)
{
    
	int sum1 = 0, sum2 = 0;
	for(int i=1;i<=n;i++){
    
		if(a[i] > mid) sum1 += a[i] - mid;
		else sum2 += mid - a[i];
	}
	
	int ans = 0;
	if(cost3 < cost1 + cost2)
	{
    
		if(sum1 >= sum2){
    
			ans += sum2 * cost3;
			sum1 -= sum2;
			ans += sum1 * cost2;
		}
		else
		{
    
			ans += sum1 * cost3;
			sum2 -= sum1;
			ans += sum2 * cost1;
		}
	}
	else
	{
    
		ans += sum1 * cost2 + sum2 * cost1;
	}
	return ans;
}

signed main(){
    
	Ios;
	cin >> n >> cost1 >> cost2 >> cost3;
	for(int i=1;i<=n;i++) cin >> a[i];
	
	int l = 0, r = 1e9;
	while(l < r)
	{
    
		int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) > check(rmid)) l = lmid + 1;
		else r = rmid - 1;
	}
	cout << check(l) << endl;
	
	return 0;
}

例2，P3745 [六省联考 2017] 期末考试 (+贪心)

Link
有 $n$ 位同学参加了全部的 $m$ 门课程的期末考试，等待成绩的公布。

第 $i$ 位同学希望在第 $t_i$ 天或之前得知所有课程的成绩。如果在第 $t_i$ 天，有至少一门课程的成绩没有公布，他就会等待最后公布成绩的课程公布成绩，每等待一天就会产生 $C$ 不愉快度。

对于第 $i$ 门课程，按照原本的计划，会在第 $b_i$ 天公布成绩。

有如下两种操作可以调整公布成绩的时间:

1. 公布课程 $X$ 成绩的时间推迟一天，公布课程 $Y$ 成绩的时间提前一天；每次操作产生 $A$ 不愉快度。
2. 学科 $Z$ 的出成绩时间提前一天；每次操作产生 $B$ 不愉快度。

通过若干次操作，使得总的不愉快度之和最小，输出最小的不愉快度之和。

$1\le n,m,t_i,b_i\le 10^5,0\le A,B,C\le 10^5$

思路
如果最后一门课程公布的时间太晚的话，那么 n 位同学等待时间就很大；如果最后一门课程公布的时间太早的话，需要花费更多来调度。所以总的花费对最后一门课程公布的时间呈中间凹的单峰函数。可以通过三分最后一门课程公布的时间来找到最小花费。

check时贪心操作，对于当前最后一门公布的时间已知，那么所有同学等待的时间便是固定的，关键在于如何调度使得花费最小。如果说，交换的花费比减小的花费少的话，就尽可能交换，实在不行再减小。

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll __int128

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N], b[N];
int A, B, C;

ll check(int ddl)
{
    
	ll sum = 0;
	for(int i=1;i<=n;i++){
    
		if(ddl > a[i]) sum += C*(ddl - a[i]);
	}
	
	if(B < A)
	{
    
		for(int i=1;i<=m;i++)
			if(b[i] > ddl) sum += B*(b[i] - ddl);
	}
	else
	{
    
		ll s = 0;
		for(int i=1;i<=m;i++)
			if(b[i] < ddl) s += ddl - b[i];
		for(int i=1;i<=m;i++)
		{
    
			if(b[i] > ddl)
			{
    
				int x = b[i] - ddl;
				if(s > x) s -= x, sum += A*x;
				else{
    
					sum += A*s;
					x -= s;
					s = 0;
					sum += B*x;
				}
			}
		}
	}
	return sum;
}

void print(ll x)
{
    
	if(x > 9) print(x / 10);
	putchar('0' + x%10);
}

signed main(){
    
	Ios;
	cin >> A >> B >> C;
	cin >> n >> m;
	for(int i=1;i<=n;i++) cin >> a[i];
	for(int i=1;i<=m;i++) cin >> b[i];
	
	int l = 1, r = 1e5;
	while(l < r)
	{
    
		int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) > check(rmid)) l = lmid + 1;
		else r = rmid - 1;
	}
	print(check(l));
	
	return 0;
}

其实，这题可以用前缀和提前预处理出每个截止日期的花费，然后O(1)判断。所以可以直接枚举或者用三分再优化。

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int unsigned long long

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N], b[N];
int cnt1[N], cnt2[N];
int A, B, C;
int suma[N], sumb[N];

signed main(){
    
	Ios;
	cin >> A >> B >> C;
	cin >> n >> m;
	for(int i=1;i<=n;i++) cin >> a[i];
	sort(a+1, a+n+1);
	for(int i=1;i<=n;i++) suma[i] = suma[i-1] + a[i];
	
	for(int i=1;i<=m;i++) cin >> b[i];
	sort(b+1, b+m+1);
	for(int i=1;i<=m;i++) sumb[i] = sumb[i-1] + b[i];
	
	int mina = 1e18;
	int idx1 = 0, idx2 = 0;
	for(int i=1;i<=b[m];i++)
	{
    
		while(idx1 + 1 <= n && a[idx1 + 1] <= i) idx1 ++;
		while(idx2 + 1 <= m && b[idx2 + 1] <= i) idx2 ++;
		
		int ans = C * (idx1 * i - suma[idx1]);
		int left = 0, need = 0;
		left = idx2 * i - sumb[idx2];
		need = sumb[m] - sumb[idx2] - (m-idx2)*i;
		if(A<B)
		{
    
			if(left > need) ans += need*A;
			else{
    
				ans += left*A;
				need -= left;
				ans += need*B;
			}
		}
		else ans += need * B;
		
		mina = min(mina, ans);
	}
	cout << mina << endl;
	
	return 0;
}

例3，P4040 [AHOI2014/JSOI2014] 宅男计划 (+贪心)

Link
一共 n 种食物，每种食物有价格 $p_i$ 和 保质期 $s_i$。

第 i 种食物将在买来之后的第 $s_i$ 天过期，比如今天买了一份保质期为 1 天的食物，那么必须在今天或者明天吃掉，保质期为 0 天必须在购买当天吃掉。

现在有 $m$ 块钱。每次点外卖需要付运费 $f$ 元，可以带来任意多份食物。
问，在满足每天至少吃一顿的情况下，最多可以点多少天？

$1\le n\le 200,0\le s_i\le 10^{18},1\le f,p_i,m\le 10^{18}$

思路
当点外卖的次数较少时，其可能要选择保质期长但较贵的食物，购买的食物数量减少；当点外卖的次数较多时，其需要多付运费，导致其购买的食物数量减少。所以只有当点外卖的次数到某个中间值的时候，其买的食物最多。购买的食物呈中间凸的单峰函数。
所以可以三分点外卖的次数，求出购买食物的最大数量。

check函数中，当点外卖的次数固定下来时，需要贪心的考虑每次点哪些外卖。
对于 k 次订购，每次肯定都按最佳策略订，所以前面点的种类和个数都是相同的，只有最后某种不能买 k 次了，有一些次订购多了这种。
把所有外卖按照价格从小到大排序，价格相同时保质期较长的放在前面，每次判断当前种类当 k 次订购都点时最多能点几份，同时还有保质期限制。
如果发现当前钱数对于 k 次订购一份都点不了时，说明后面都点不了了，退出。
只能订购某种外卖若干次以便将所有钱花完，到不了 k 次了。

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll unsigned long long

const int N = 200010, mod = 1e9+7;
int T, n, m;
int f;
PII a[N];

bool cmp(PII a, PII b){
    
	if(a.fi != b.fi) return a.fi < b.fi;
	return a.se > b.se;
}

int check(ll k)
{
    
	if(k*f >= m || k == 0) return 0;
	
	ll w = m - k*f;
	ll ans = 0;
	
	//每次订购时都买这种，每次尽可能买多份，以使得花费最少，买的最多
	int now = 0;
	for(int i=1;i<=n;i++)
	{
    
		if(a[i].se >= now)
		{
    	
			if(w < k*a[i].fi) break; //如果当前价格一份也不能买，那么后面都不能买，退出
			else
			{
    
				ll fen = min(w/(k*a[i].fi), (ll)a[i].se - now + 1); //每次订购时能买的份数，钱数或者保质期限制 
				w -= fen * k * a[i].fi;
				now += fen;
				ans += k * fen;
			}
		}
	}
	
	//剩下的钱虽然不能每次订购都买一份了，但是可能在某些次订购的时候多买一份，求出多买的份数
	for(int i=1;i<=n;i++)
	{
    
		if(a[i].se >= now)
		{
    
			ll fen = w/a[i].fi;
//			w -= fen * a[i].fi;
//			now += fen;
			ans += fen;
			break;
		}
	}
	return ans;
}

signed main(){
    
	Ios;
	cin >> m >> f >> n;
	for(int i=1;i<=n;i++) cin >> a[i].fi >> a[i].se;
	
	sort(a+1, a+n+1, cmp);
	
	int l = 0, r = m/f;
	while(l < r)
	{
    
		int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) < check(rmid)) l = lmid + 1;
		else r = rmid - 1;
	}
	cout << check(l);
	
	return 0;
}

---

计算几何中的三分

例1，4180. 灯泡

Link

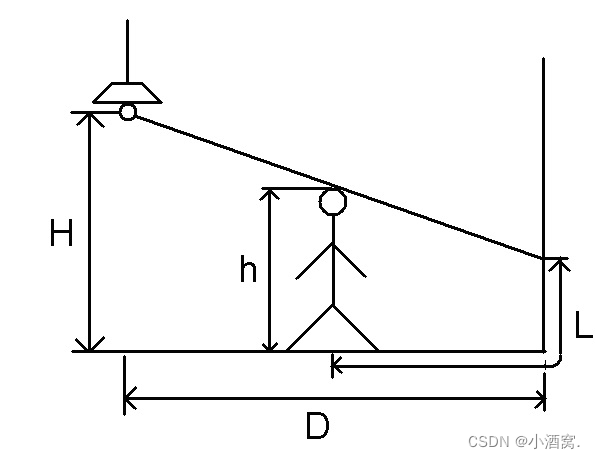
给定 $H,h,D$，人在 D 上移动，左上角为灯泡。
求影子 $L$ 的最长长度。

思路
当人太靠左时，影子可能不会投射到右面的墙上，影子的长度很短；当人太靠右时，影子会过多投射到墙上，最长长度为人的身高。而在中间某个位置时，影子在地面上拉长并可能有一部分投射到墙上，总长度最长。
所以影子的长度随着人的位置呈中间凸的单峰函数，三分人的位置求峰值。

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
double H, h, D;

int bi(double x, double y){
     //减少精度误差 
	if(fabs(x - y) < 1e-6) return 0;
	if(x > y) return 1;
	return -1;
}

double check(double x)
{
    
	if(bi(x, 0) == 0) return 0;
	
	if(bi(x + x*h/(H-h), D) <= 0) return x*h/(H-h); //影子未投射到墙上 
	
	double ans = H - D*(H-h)/x;
	return D - x + ans;
}

signed main(){
    
	Ios;
	cin >> T;
	while(T--)
	{
    
		cin >> H >> h >> D;
		
		double l = 0, r = D;
		for(int i=1;i<=1000;i++)
		{
    
			double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
			if(check(lmid) < check(rmid)) l = lmid;
			else r = rmid;
		}
		printf("%.3f\n", check(l));
	}
	
	return 0;
}

例2，Stealing a Cake

Link
在二维坐标上，有点 $S(x,y)$、圆心为 $(x_0,y_0)$、半径为 $r$ 的圆、一个相对顶点为 $(x_1,y_1),(x_2,y_2)$ 边与坐标轴平行的矩形。
保证三种图形互不重叠。
问，从起点出发，触及圆周任一点后，再触及矩形的最小路径长度为多少？

$10^4\le x_t,y_t\le 10^4$

思路
以任意位置为分界线将圆分为两个半圆，点 S 到圆上一点再到矩形的距离一定满足，在一个半圆上先增后减，在另一个半圆上先减后增。
按照圆心角 $[0,\pi ]$ 和 $[\pi ,2\pi ]$ 分成两个半圆，对于每个半圆，三分其圆心角，求峰值（最小值）。
圆心角 du 固定了，那么圆上的点为 x = x0 + r * cos(du), y = y0 + r * sin(du)，到矩形的最小距离为：到矩形四个边距离的最小值。

Code

//http://acm.hdu.edu.cn/showproblem.php?pid=4454
#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)

const int N = 200010, mod = 1e9+7;
const double PI = acos(-1);
int T, n, m;
struct node{
    
	double x, y;
};
double r;
node st, c, a[N];

int bi(double x, double y){
    
	if(fabs(x - y) <= 1e-6) return 0;
	if(x > y) return 1;
	return -1;
}

double dis(node a, node b){
    
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

double distoline(node p, node a, node b)
{
    
	double ap = (b.x-a.x)*(p.x-a.x)+(b.y-a.y)*(p.y-a.y);
    if(bi(ap, 0) <= 0) return sqrt((p.x-a.x)*(p.x-a.x)+(p.y-a.y)*(p.y-a.y));//最短为ap
    double ab = (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
    if(bi(ap, ab) >= 0) return sqrt((p.x-b.x)*(p.x-b.x)+(p.y-b.y)*(p.y-b.y));//最短为bp
    double r = ap/ab;
    double px = a.x+(b.x-a.x)*r;
    double py = a.y+(b.y-a.y)*r;
    return sqrt((p.x-px)*(p.x-px)+(p.y-py)*(p.y-py));//垂线距离
}

double check(double du)
{
    
	double x = c.x + r * cos(du), y = c.y + r * sin(du);
	node pos = {
    x, y};
	double mina = 1e18;
	for(int i=1;i<=4;i++)
		mina = min(mina, distoline(pos, a[i], a[i%4 + 1]));
	return mina + dis(pos, st);
}

double pd(double l, double r)
{
    
	for(int i=1;i<=100;i++)
	{
    
		double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) > check(rmid)) l = lmid;
		else r = rmid;
	}
	return check(l);
}

signed main(){
    
	Ios;
	while(cin >> st.x >> st.y && !(bi(st.x, 0) == 0 && bi(st.y, 0) == 0))
	{
    
		cin >> c.x >> c.y;
		cin >> r;
		
		cin >> a[1].x >> a[1].y >> a[3].x >> a[3].y;
		if(bi(a[1].y, a[3].y) < 0) swap(a[1], a[3]);
		a[2] = {
    a[3].x, a[1].y};
		a[4] = {
    a[1].x, a[3].y};
		
		double ans = 1e18;
		ans = min(ans, pd(0, PI));
		ans = min(ans, pd(PI, 2*PI));
		printf("%.2lf\n", ans);
	}
	
	return 0;
}

---

三分套三分

如果在两个变量都未知的情况下，整体是可以三分的，然后当一个变量确定的情况下，另一个变量也是可以三分的，那么就可以用三分套三分求解，先三分一个值，然后在该值确定的情况下，三分另一个值，得到最优解传回来用于第一个三分，直到得到最优解。

例1，Line belt

Link
在一个二维平面上有两条线段 AB 和 CD，在 AB 上的移动速度是 P，在 CD 上是 Q，在平面上的其他区域以速度 R 移动。
问，从 A 到 D 需要多长时间？

$0<=Ax，Ay，Bx，By，Cx，Cy，Dx，Dy<=1000$
$1<=P，Q，R<=10$

思路
最佳的策略一定是从 A 点移动到线段 AB 的某个位置，然后到线段 CD 的某个位置接着到 D 点。
但是到哪个位置不知道，两个变量。
可以看出，整体的时间一定是先减少后增加的，最优解在中间的某个位置，所以整体是可以三分的。
同时，当在线段 AB 的位置确定的话，到达 CD 的某个位置后到 D 点所要的时间也是先减少后增加的，也可以三分求出最优解。
所以，可以三分到线段 AB 的位置，在该位置确定的情况下，三分到线段 CD 上的位置，得到此时最优解传回去用以第一个三分，最终得到最优解。

Code

//http://acm.hdu.edu.cn/showproblem.php?pid=3400
#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)

const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
    
	double x, y;
};
node a, b, c, d, e, f;
double P, Q, R;

double dis(node a, node b){
    
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

double check1(node e, node f)
{
    
	return dis(e, f)/R + dis(f, d)/Q;
}

double check(node e)
{
    
	double lx = c.x, ly = c.y, rx = d.x, ry = d.y;
	for(int i=1;i<=500;i++)
	{
    
		double lmidx = lx + (rx - lx)/3, rmidx = rx - (rx - lx)/3;
		double lmidy = ly + (ry - ly)/3, rmidy = ry - (ry - ly)/3;
		
		if(check1(e, {
    lmidx, lmidy}) > check1(e, {
    rmidx, rmidy})) lx = lmidx, ly = lmidy;
		else rx = rmidx, ry = rmidy;
	}
	return dis(a, e)/P + check1(e, {
    lx, ly});
}

signed main(){
    
	Ios;
	cin >> T;
	while(T--)
	{
    
		cin >> a.x >> a.y >> b.x >> b.y;
		cin >> c.x >> c.y >> d.x >> d.y;
		
		cin >> P >> Q >> R;
		
		double lx = a.x, ly = a.y, rx = b.x, ry = b.y;
		for(int i=1;i<=500;i++) //当复杂度不确定时，可以按照所剩余的时间设置三分次数 
		{
    
			double lmidx = lx + (rx - lx)/3, rmidx = rx - (rx - lx)/3;
			double lmidy = ly + (ry - ly)/3, rmidy = ry - (ry - ly)/3;
			
			if(check({
    lmidx, lmidy}) > check({
    rmidx, rmidy})) lx = lmidx, ly = lmidy;
			else rx = rmidx, ry = rmidy;
		}
		printf("%.2lf\n", check({
    lx, ly}));
	}
	return 0;
}

例2，1420. 通电围栏

Link
在一个二维坐标系中，给定 n 个线段的端点坐标。
要求找到一个位置，使其到 n 个线段的距离之和最小。

$1\le n\le 150,$
$0\le x_1,y_1,x_2,y_2\le 100$

思路
容易想到，在从最佳位置向外扩散的过程中，该位置到线段的距离之和不断增大，中间小，四周大，整体可以三分。
同时，当横坐标确定的情况下，对于纵坐标的位置也是中间小，两边大，纵坐标也可以三分。
所以，三分横坐标，在横坐标确定的情况下，三分纵坐标得到最优解，返回来用于继续判断。

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)

const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
    
	double x, y;
}st[N], en[N];

double bi(double x, double y){
    
	if(fabs(x - y) < 1e-6) return 0;
	if(x > y) return 1;
	return -1;
}

double distoline(node p, node a, node b)
{
    
	double ap = (b.x-a.x)*(p.x-a.x)+(b.y-a.y)*(p.y-a.y);
    if(bi(ap, 0) <= 0) return sqrt((p.x-a.x)*(p.x-a.x)+(p.y-a.y)*(p.y-a.y));//×î¶ÌΪap
    double ab = (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
    if(bi(ap, ab) >= 0) return sqrt((p.x-b.x)*(p.x-b.x)+(p.y-b.y)*(p.y-b.y));//×î¶ÌΪbp
    double r = ap/ab;
    double px = a.x+(b.x-a.x)*r;
    double py = a.y+(b.y-a.y)*r;
    return sqrt((p.x-px)*(p.x-px)+(p.y-py)*(p.y-py));//´¹Ïß¾àÀë
}

double check1(node p)
{
    
	double sum = 0;
	for(int i=1;i<=n;i++){
    
		sum += distoline(p, st[i], en[i]);
	}
	return sum;
}

double check(double x, int k)
{
    
	double l = 0, r = 100;
	for(int i=1;i<=200;i++)
	{
    
		double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check1({
    x, lmid}) > check1({
    x, rmid})) l = lmid;
		else r = rmid;
	}
	if(k) printf("%.1f %.1f\n", l, check1({
    x, l}));
	return check1({
    x, l});
}

signed main(){
    
	Ios;
	cin >> n;
	
	for(int i=1;i<=n;i++){
    
		double x, y; cin >> x >> y;
		st[i] = {
    x, y};
		cin >> x >> y;
		en[i] = {
    x, y};
	}
	
	double l = 0, r = 100;
	for(int i=1;i<=200;i++)
	{
    
		double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid, 0) > check(rmid, 0)) l = lmid;
		else r = rmid;
	}
	printf("%.1f ", l);
	check(l, 1);
	
	return 0;
}

---

真题

1，D Arithmetic Sequence (21济南站)

Link
给定长度为 n 的数列，每个位置都是整数。
每次操作可以使一个元素 +1 或 -1。
问，最小用多少次操作能将该数列变为等差数列？

$1\le n\le 2\times 10^5,0\le \mid a_i\mid \le 10^{13}$

思路
这场比赛去打了，当时看到的时候没有一点思路，没有刷过三分专题，也没往三分上想。。
然后刷过三分之后再看这道题，第一眼感觉是，首项和公差都不知道，两个变量未知，而整体的答案是先减小后增大，就想三分套三分。先三分首项再三分公差，样例能过，但是交一发超时。
2e5 * 2log1e13 * 2log1e13 超过 1e9，只能挂一个 log，也就是说要优化掉一个三分。

公差肯定要三分，那么能不能把三分首项优化掉呢？
也就是说，在已知公差的情况下，能否O(n)求出变成等差数列的操作次数？

是可以的。
对于一个等差数列来说，其每一项分别为 a1, a1+d, a1+2d, a1+3d, …, a1+(n-1)d。
如果把后面的公差减掉，那么每一项都是 a1。
而现在如果把当前的数列减去后面的公差，会得到n个数：x1, x2, x3, x4, …, xn。
这 n 个数其实应该是相同的，都是首项。
也就是要确定一个数，让这 n 个数都变成这个数的操作次数最少，也就是要找一个 t，使得：$|x_1-t|+|x_2-t|+|x_3-t|+...+|x_n-t|$ 最小。
货仓选址问题，最佳的 t 为这 n 个数的中位数，找到中位数便是首项，绝对值之和便是操作次数。
那么如何 O(n) 求中位数呢？可以用 nth_element()函数。

for(int i=0;i<n;i++) cin >> a[i];
nth_element(a, a+k, a+n); //使第k小整数就位 
cout << a[k]; //调用第k小整数
或者
for(int i=1;i<=n;i++) cin >> a[i];
nth_element(a+1, a+k, a+n+1);//使第k小整数就位 
cout << a[k]; //调用第k小整数

另外注意可能爆 long long，要用 __int128。

Code

//https://pintia.cn/problem-sets/1459829212832296960/problems/1459829264400629763
#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll __int128

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
ll b[N];

ll check(int mid)
{
    
	ll st = mid;
	for(int i=1;i<=n;i++)
	{
    
		b[i] = a[i] - st;
		st += mid;
	}
	
	nth_element(b+1, b+(n+1)/2, b+n+1);
	int ans = b[(n+1)/2];
	
	ll sum = 0;
	for(int i=1;i<=n;i++){
    
		if(b[i] > ans) sum += b[i] - ans;
		else sum += ans - b[i];
	}
	return sum;
}

void print(ll x)
{
    
	if(x > 9) print(x / 10);
	putchar('0' + x % 10);
}

signed main(){
    
	scanf("%lld", &n);
	for(int i=1;i<=n;i++) scanf("%lld", &a[i]);
	
	int l = -2e13, r = 2e13;
	while(l < r)
	{
    
		int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
		if(check(lmid) > check(rmid)) l = lmid + 1;
		else r = rmid - 1;
	}
	
	print(check(l));
	
	return 0;
} 

2，Link with Arithmetic Progression (22牛客多校)

Link
给定长度为 n 的数列。
每次操作可以修改其中一个元素，花费为 $(a_i-a_i^{\prime }{)}^2$。（可以修改为任意实数）
问，将数列变为等差数列的最小花费？

$1\le T\le 1000,3\le n\le 10^5,|a_i|\le 10^9,\sum n<1e6$

思路
题目和上一题很类似，同样三分公差，然后 O(n) 求出最小花费。
同样，都减去后面的公差后，变为 x1, x2, x3, …, xn。

现在我们要使得 $(x_1-t{)}^2+(x_2-t{)}^2+(x_3-t{)}^2+...+(x_n-t{)}^2$ 最小。

而 $x_i$ 已知，所以上式就是一个开口向上的二次函数，直接找对称轴求最小值或者用 $\frac{4ac-b^2}{4a}$。
或者，从上式直接看出将 t 赋值为 $x_i$ 总和的平均值时最优。

比较奇怪的是，double 超时，换成 long double 就过了。

Code

#include<bits/stdc++.h>
using namespace std;

#define int long long
#define PII pair<int,int>
#define endl '\n'
#define double long double

const int N = 200010, mod = 1e9+7;
int T, n, m;
double a[N], t[N], c[N];

namespace GTI
{
    
    char gc(void)
       {
    
        const int S = 1 << 16;
        static char buf[S], *s = buf, *t = buf;
        if (s == t) t = buf + fread(s = buf, 1, S, stdin);
        if (s == t) return EOF;
        return *s++;
    }
    int gti(void)
       {
    
        int a = 0, b = 1, c = gc();
        for (; !isdigit(c); c = gc()) b ^= (c == '-');
        for (; isdigit(c); c = gc()) a = a * 10 + c - '0';
        return b ? a : -a;
    }
}
using GTI::gti;

double check(double d)
{
    
	double x = a[1], sum = 0;
	for(int i=1;i<=n;i++)
	{
    
		t[i] = a[i] - x;
		x += d;
		sum += t[i];
	}
//	sum /= n;
//	
//	double ans = 0;
//	for(int i=1;i<=n;i++)
//		ans += (t[i] - sum) * (t[i] - sum);
//	return ans;
	double a = 0, b = 0, c = 0;
    for(int i=1;i<=n;i++)
    {
    
        a ++;
        b -= 2*t[i];
        c += t[i] * t[i];
    }
    
//    double ans = -b/(2*a);
//    return a*ans*ans + b*ans + c;
	return c - b*b/(4*a);
}

signed main(){
    
	cin >> T;
	while(T--)
	{
    
		n = gti();
		for(int i=1;i<=n;i++) a[i] = gti();
		
		double l = -1e9, r = 1e9;
		while(fabs(r - l) > 1e-10)
		{
    
			double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
			if(check(lmid) > check(rmid)) l = lmid;
			else r = rmid;
		}
		printf("%.10Lf\n", check(l));
	}
	
	return 0;
}

总结

总之，三分就是用于，在不确定最优解位置，但确实有峰值的情况下，求出最优解。
时间复杂度 $O(2lo{g}_3^n)$。